一.导学

  • 以人脸智能为例

    智能化水平最高

    相关业务落地更深入

    包括：目标检测、关键点定位、活体检测、相似性度量

二.深度学习基础

2.1 卷积神经网基本概念

  • 什么是人工神经网络？

    人工智能领域—>机器学习

    神经元—>网络节点

    神经网络：输入层、输出层、隐藏层

  • 什么是感知器

    第一个具有完整算法描述的神经网络学习算法（称为感知器的学习算法：PLA）

    任何线性分类或线性回归问题都可以用感知器来解决

  • 多层感知器(MLP, Multilayer Perception) 也叫人工神经网络(ANN, Artificial Neural Network)

  • 什么是深度学习？

    含有多隐层的多层感知器就是一种深度学习结构

    p1-深度学习结构

  • 总结

    神经元—>感知器—>神经网络—>深度学习

2.2 前向运算

  • 定义

    计算输出值的过程称为前向传播

    p2-前向运算过程

2.3 反向传播（Backpropagation, BP）

  • 神经网络（参数模型）训练方法，1986年由Rumelhar和Hinton等人提出

  • 解决神经网络优化的问题

  • 计算输出层结果与真实值之间的偏差来进行逐层调节参数（梯度下降）

    （神经网络 = 网络结构 + 参数）

  • 神经网络的训练是一个不断迭代过程

    p3-反向传播过程

  • 参数优化问题（迭代）

    导数和学习率（解决方法）完成梯度下降

2.4 反向传播的一些概念

2.4.1 导数

导数是变化率、是切线的斜率、是瞬时速度、加速度

2.4.2 方向导数

函数在某点无数个切线的斜率的定义，每一个切线都代表着一个变化的方向

2.4.3 偏导数

多元函数降维时的变化，比如二元函数固定y，只让x单独变化，从而看成是关于x的一元函数的变化来研究

2.4.4 梯度

函数在A点无数个变化方向中变化最快的方向

记为：∇ f 或者 gradf = (偏导数)

2.5 梯度下降算法

  • 选择合适的步长/学习率

  • 局部最优解

2.6 常见的深度学习模型

  • 卷积神经网（CNN）
  • 循环神经网（RNN）
  • 自动编码机（Autoencoder）
  • 受限玻尔兹曼机
  • 深度信念网络

三.卷积神经网

3.1 卷积神经网内容概括

  • 大体如下

    p4-卷积神经网内容概况

3.2 基本组成单元

  • 什么是卷积神经网

    以卷及结构为主，搭建起来的深度网络

    例如：将图片作为网络的输入，自动提取特征，并且对图片的变形等具有高度不变形

  • 组成单元

    卷积 -> 池化 -> 激活 -> BN -> LOSS -> 其它层

3.3 卷积运算的定义

  • 对图像和滤波矩阵做内积（逐个元素相乘并求和）的操作

    • 滤波器（卷积）
    • 每种卷积对应一种特征
    • lm2col实现卷积运算

  • 下图为卷积的算法示例

    p5-卷积示例

3.4 卷积中的重要参数

  • 卷积核

    最常用2D卷积核（k_w*k_h）

    权重和偏置项

    常用卷积核：1*1, 3*3, 5*5 (保护位置信息，padding时对称)

3.5 权值共享与局部连接

  • 卷积运算作用在局部（局部感受野）

  • Featrue map使用同一个卷积核运算后得到一种特征

  • 多种特征采用多个卷积核（channel）

  • 权值共享：减少参数量

3.6 卷积核与感受野

  • 卷积核

    若有一个5*5的图像，使用5*5的卷积核 -> 得到1*1，这和使用两个3*3的卷积核进行两次卷积的结果一样，即2个3*3 = 1个5*5 （卷积核）

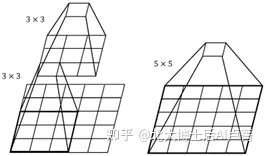
    p6-3*3卷积核卷积后

    以上图为例，若使用5*5卷积核进行卷积，有5*5=25个参数；若使用2个3*3卷积核进行卷积，有3*3*2=18个参数，减少了7个参数，但最后得到的效果一致

    总结：使用更小的卷积核代替大卷积核可以减少计算量，加深网络

  • 感受野

    根据上面的例子，我们说3*3的卷积核可满足5*5的感受野

  • 计算卷积核参数量（parameters）

    (k_w * k_h * ln_channel + 1) * Out_channel

  • 计算卷积的计算量（FLOPS）

    ln_w * ln_h *(k_w * k_h * ln_channel + 1) * Out_channel

3.7 步长与Pad

  • 步长（stride）

    在下采样过程中如何计算输出的Feature Map？

    p7-卷积的Feature Map

  • Pad

    确保Feature Map整数倍的变化

    F=3 -> zero pad with 1

    F=5 -> zero pad with 2

    F=7 -> zero pad with 3

    这里pad指的是从卷积核第一个点向上（左）所到达的坐标，要扩充pad层，如下图所示

    p8-卷积的pad

    注意：参数量不变，计算量增加

3.8 卷积的定义与使用（tensorflow）

简单示例

1
2
3
4
5
6
7
8
9
10
11
12
# 权值项 'weight'为name，后面为shape（形状）
filter_weight = tf.get_variable('weight',[5,5,3,16],
initializer = tf.truncated_normal_initializer(stddev=0.1))
# 偏置项
biases = tf.get_variable('biases',[16],initializer=tf.constant_initializer(0.1))
# 输入数据，卷积核参数，strides参数，padding参数
conv = tf.nn.conv2d(input, filter_weight, strides[1,1,1,1], padding='SAME')
# 结果与偏置项相加
bias = tf.nn.bias_add(conv, biases)

# 输入数据，输出channel数量，卷积核大小
net = slim.conv2d(input_x,64,[3,3],scope='conv1_1')

3.9 池化层

  • 池化（无参）：对输入的特征图进行压缩

    特征图变小，简化网络计算复杂度

    进行特征压缩，提取主要特征

    增大感受野

    p9-池化

  • 常见的池化策略

    最大池化（Max Pooling）

    平均池化（Average Pooling）

    随机池化（Stochastic Pooling）

3.10 激活层

  • 激活函数（非线性、单调性、可微性）

    增加网络的非线性，进而提升网络表达能力

    Sigmoid、Tanh、ReLU等

  • Sigmoid函数

    p10-Sigmoid函数

    取值范围0~1（因此可以用来表达概率）

    缺点：出现 梯度弥散/梯度饱和，输出不是以0为中心（可以总体减0.5）

  • Tanh（双曲正切函数）

    p11-Tanh函数

    完全可微分，可对称，对称中心在原点

  • ReLu（修正线性单元 Rectified Linear Unit）

    p12-ReLU

    生物学启发（只有输入超出阈值时神经元才激活）

    函数形式简单，正数时不存在梯度饱和

    缺点：负数时会死掉

3.11 BatchNorm层

  • 通过一定的规范化手段，把每层神经网络任意神经元输入值分布拉回到均值为0、方差为1的标准正态分布

    优点：减少参数人为选择、减少对学习率要求、可以不再使用局部响应归一化

  • Tensorflow中使用BN层

    1
    2
    3
    tf.nn.batch_normalization
    tf.layers.batch_normalization
    tf.contrib.layers.batch_norm

3.12 全连接层

  • 连接所有特征，将输出值送给分类器（例如softmax）。即全连接层的每一个结点都与上一层的所有结点相连。

    可将网络输出变成一个向量

    可以采用卷积代替全连接层

    全连接层是尺度敏感的

    配合使用dropout层

3.13 Dropout层

  • 训练过程中，随机丢弃一部分输入，将对应的参数置为0

    缓解过拟合问题（取平均、减少神经元之间复杂的共适应关系）

    p13-Dropout层

3.14 损失层

  • 损失函数

    用来评估模型的预测值和真实值的不一致的程度

    经验风险最小：交叉熵损失、softmax loss

    结构风险最小：l0，l1范式

  • 损失层定义了使用的损失函数，通过最小化损失来驱动网络的训练

    分类任务损失：交叉熵损失

    回归任务损失：L1损失，L2损失

交叉熵损失

  • log-likelihood cost

    非负性、当真实输出a与期望输出y接近，代价函数接近于0

    p14-交叉熵损失-代价函数

L1、L2、Smooth L1损失

  • Smooth L1是L1的变形，用于Faster RCNN、SSD等网络计算损失

    p15-L1、L2、Smooth L1损失

3.15 LeNet与AlexNet

  • LeNet

    1998年由LeCun提出，用于解决手写数字识别，MNIST

  • AlexNet

    网络结构更深，通过GPU完成训练，参数量在60M以上

3.16 ZFNet与VggNet

  • ZFNet

    在AlexNet基础上进行了细节调整（调整第一层卷积核大小为7*7，原来为11*11，设置卷积参数stride=2）

  • 特征可视化

    特征分层次体系结构（低、中、高）

    深层特征更鲁棒

    深层特征更有区分度

    深层特征收敛更慢…

  • VGGNet

    由牛津大学计算机视觉组和Google Deepmind共同设计。

    为了研究网络深度对模型准确度的影响，并采用小卷积堆叠的方式来搭建整个网络结构。

    参数量138M，模型大小>500M

    特点：

    网络结构更规整、简单，全部使用3*3的小型卷积核和2*2的最大池化层。

    每次池化后 Feature Map 宽高降低一半，通道数量增加一倍。

    网络层数更多、结构更深、模型参数量更大。

3.17 Inception-卷积神经网如何减少参数量和计算量

  • GoogleNet / Inception v1

    在设计网络结构时，不仅强调网络的深度，也要考虑网络的宽度，并将这种结构定义为 Inception 结构。

    这个模型说明：更多的卷积、更深的层次也可以获得更好的结构。

    参数量6.8M，模型大小50M

    特点：

    更深的网络结构

    两个LOSS层，降低过拟合风险

    考虑网络宽度

    巧妙地利用1*1卷积核来进行通道降维，减少计算量

3.18 从卷积角度思考，如何减少网络中的计算量

  1. 小卷积核来对大卷积核进行拆分
  2. Stride=2代替pooling层
  3. 巧妙地利用1*1的卷积核

3.19 ResNet

2015年，由何凯明团队提出，引入跳连结构来防止梯度消失问题

  • Bottleneck：跳连结构（Short-Cut）恒等映射，解决梯度消失问题

  • BatchNorm：每个卷积后都会配合一个BatchNorm层，对数据scale和分布进行约束

  • ResNet设计特点

    核心单元简单堆叠

    跳连结构解决网络梯度消失问题

    Average Pooling层代替FC层

    BN层加快网络训练速度和收敛时稳定性

    加大网络深度，提高模型特征抽取能力

1
2
watch?v=PWbpUd7dKrM&list=PL22JdLI1-RcHzEJZtAOiNzCKucv-YvDGm&index=4
47：47