Gurobi快速入门

优化代码示例：https://www.gurobi.com/documentation/10.0/examples/python_examples.html

Gurobi中国：http://www.gurobi.cn/pic.asp

一. 安装问题

1.1 C++ / Xcode 调用 Gurobi

在官网下载安装包：可以安装完整版，包括 C++ / Python 等库文件，具体教程可以网上查阅。

我推荐使用 Python 来调用 Gurobi 接口，因为这样配置起来没那么麻烦。

下面总结使用 C++ / Xcode 编译器中导入 Gurobi 库的一些问题：

第一步，需要确定 Gurobi 的安装路径，并进入build目录，我的是/Library/gurobi1002/macos_universal2/src/build。然后进入终端，执行make命令，得到libgurobi_c++.a文件，将其移动到/Library/gurobi1002/macos_universal2/lib中。

第二步，新建 Xcode 项目，然后按照下图先配置头文件：

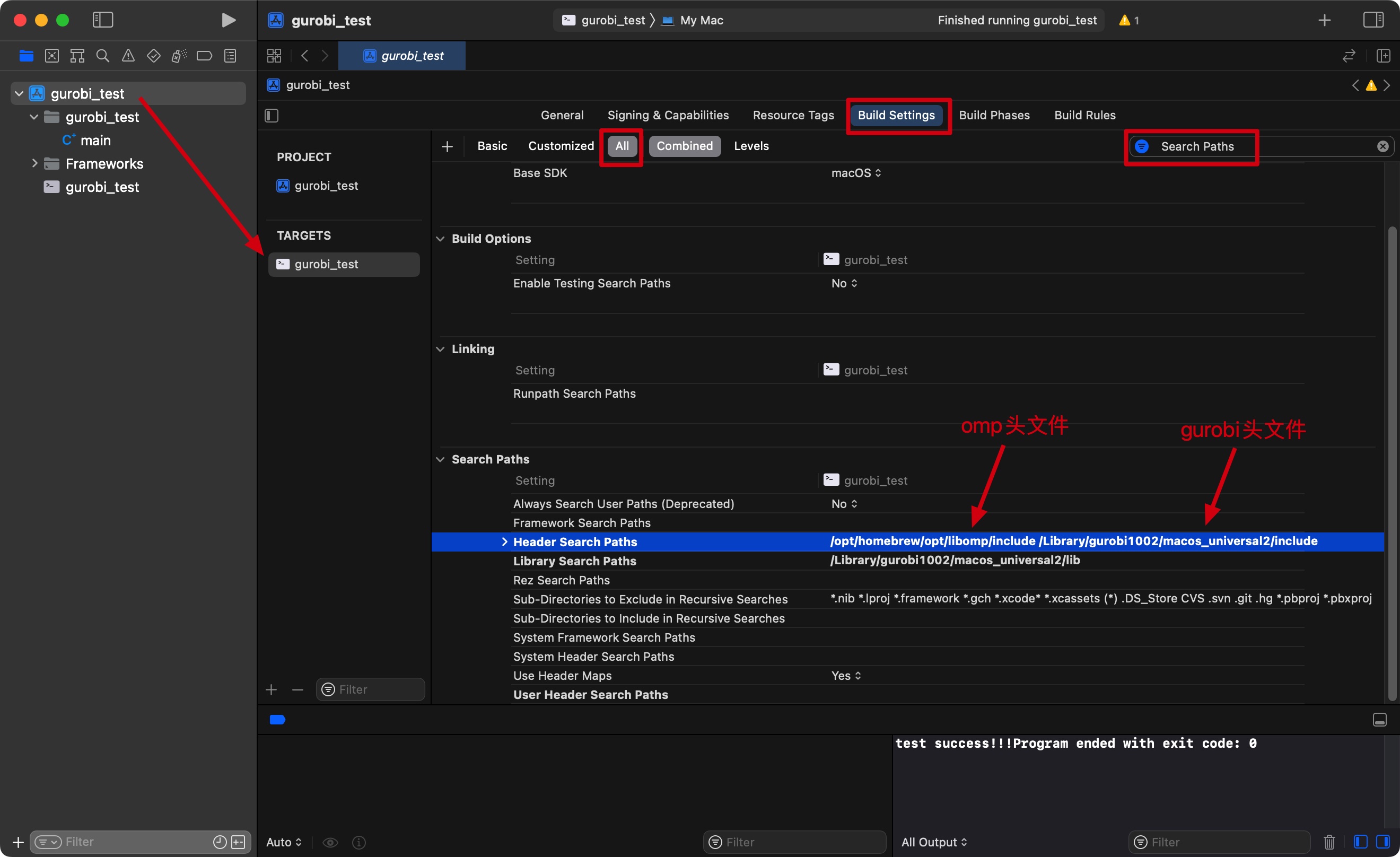
头文件配置

这里补充一个小知识：include<> 是只从 Header Search Paths 中搜索。而 include"" 则能从 Header Search Paths 和 User Header Search Paths中搜索（优先搜索当前目录下）。

第三步（很重要）是添加运行库链接文件（在/Library/gurobi1002/macos_universal2/lib目录下），如下图所示：

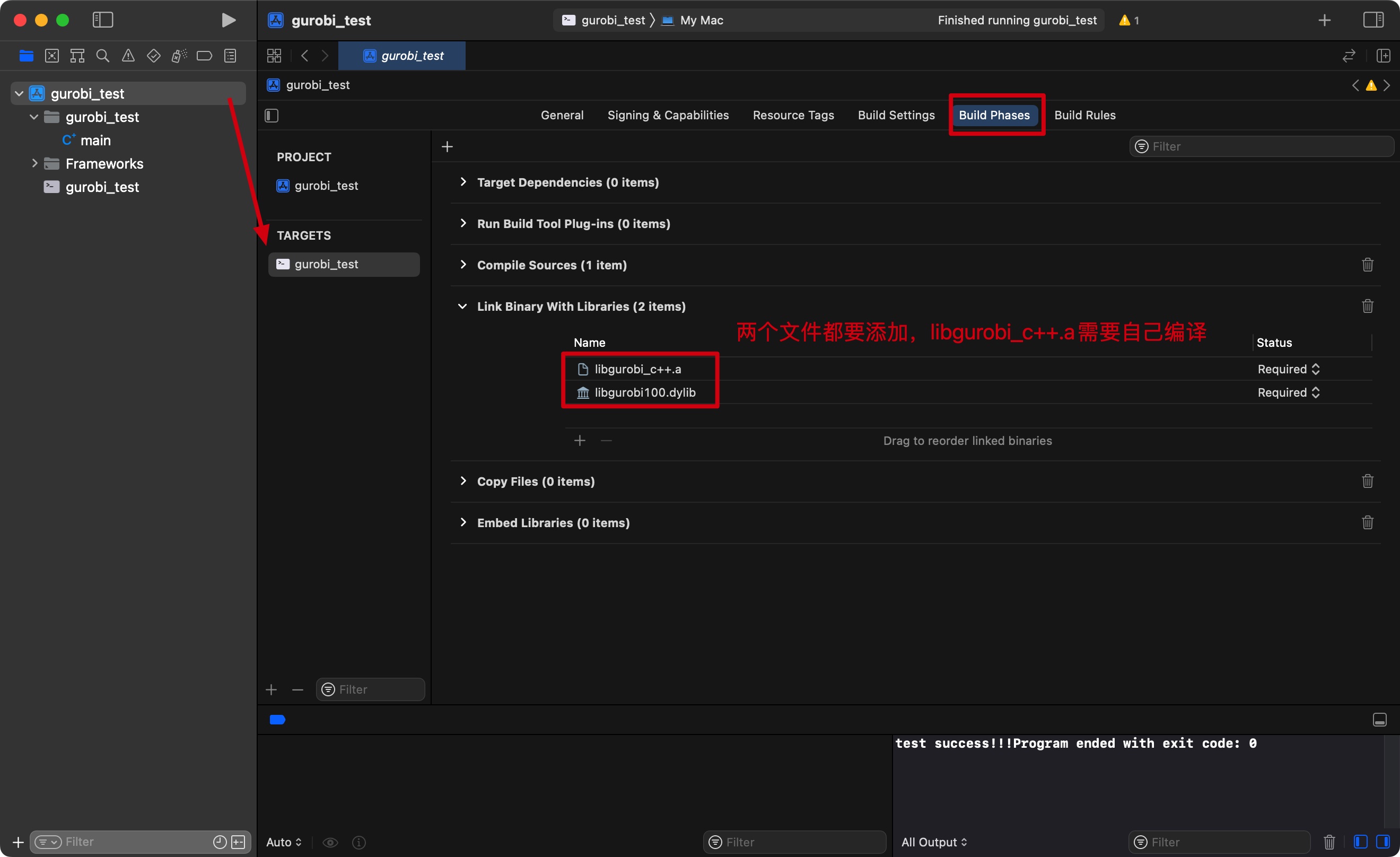
添加运行库链接文件

如果配置不对，会出现 Undefined symbol 等报错信息！

代码里一定要try-catch，基本框架如下：

#include "gurobi_c++.h"

int main(int argc, char** argv) {
    try {
        GRBEnv env = GRBEnv();
        GRBModel model = GRBModel(env);

        // 配置参数和创建变量、约束等...

        // 优化模型
        model.optimize();

        // 输出结果...
        
    } catch (GRBException& e) {
        std::cout << "Gurobi Error: " << e.getErrorCode() << ", " << e.getMessage() << std::endl;
    } catch (...) {
        std::cout << "An exception occurred." << std::endl;
    }

    return 0;
}

二. 使用入门

2.1 什么是Gurobi

Gurobi是目前数学规划（线性和凸二次规划）优化器性能领袖、性价比领袖。国内应用涵盖航空运输、电力、制造、传媒管理、生物医药、通讯和金融等领域。

其学术版本是免费的，需要提交一份 申请表 和 在线学籍验证报告 。

它可以用于求解：大规模线性问题、二次型目标问题、混合整数线性和二次型问题。

提供方便的接口，支持 C++ / Java / Python / .Net / Matlab / R 以及多种平台。

下面以 Python 语言为例。

2.2 建模过程

Problem Instance：待优化问题

Model Generator：将数据组合成模型，产生计算机模型对象

Model Instance：存在内存中的一个完整数学模型

Gurobi Optimizer：优化求解

Solution Retrieval：根据需要读取优化结果

Analysis：对结果进行分析

上面步骤循环往复，直到获取满意结果。

2.3 建模举例

2.3.1 例子1：简单的目标与约束函数

max    x + y + 2z
s.t.   x + 2y + 3z <= 4
       x + y >= 1
       x, y, z ∊ {0,1}

代码如下：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thu Jul  6 15:05:58 2023

@author: github.com/cszmzh
"""

from gurobipy import *

try:
    
    # 创建模型
    m = Model("mip1")
    
    # 创建变量 vtype指定二进制变量
    x = m.addVar(vtype=GRB.BINARY, name='x')
    y = m.addVar(vtype=GRB.BINARY, name='y')
    z = m.addVar(vtype=GRB.BINARY, name='z')
    
    # 设置目标函数
    m.setObjective(x + y + 2 * z, GRB.MAXIMIZE)
    
    # 添加约束
    m.addConstr(x + 2 * y + 3 * z <= 4, "c0")
    m.addConstr(x + y >= 1, "c1")
    
    m.optimize()
    
    # 打印结果
    for v in m.getVars():
        print('%s %g' % (v.varName, v.x)) # 最优解下，x y z的取值
    
    print('Obj: %g' % m.objVal) # 最优解下，目标函数的值

except GurobiError as e:
    print('Error code ' + str(e.errno) + ":" + str(e))
    
except AttributeError:
    print("Encountered an attribute error")

2.3.2 例子2：营养配方模型

人体需要四种营养：calories / protein / fat / sodium

食物来源：hamburger / chicken / hot dog / fries / macaroni / pizza / salad / milk / ice cream

注意：

1.营养吸收每天有上限与下限

import gurobipy as gp
from gurobipy import GRB

# STEP: 指定四种营养，并设置上下限，详见multidict的用法
categories, minNutrition, maxNutrition = gp.multidict({
    'calories': [1800, 2200],
    'protein':  [91, GRB.INFINITY],
    'fat':      [0, 65],
    'sodium':   [0, 1779]})

2.单位重量食物价格、营养成分均不同

# STEP: 定义价格
foods, cost = gp.multidict({
    'hamburger': 2.49,
    'chicken':   2.89,
    'hot dog':   1.50,
    'fries':     1.89,
    'macaroni':  2.09,
    'pizza':     1.99,
    'salad':     2.49,
    'milk':      0.89,
    'ice cream': 1.59})

# STEP: 定义营养成分
nutritionValues = {
    ('hamburger', 'calories'): 410,
    ('hamburger', 'protein'):  24,
    ('hamburger', 'fat'):      26,
    ('hamburger', 'sodium'):   730,
    ('chicken',   'calories'): 420,
    ('chicken',   'protein'):  32,
    ('chicken',   'fat'):      10,
    ('chicken',   'sodium'):   1190,
    ('hot dog',   'calories'): 560,
    ('hot dog',   'protein'):  20,
    ('hot dog',   'fat'):      32,
    ('hot dog',   'sodium'):   1800,
    ('fries',     'calories'): 380,
    ('fries',     'protein'):  4,
    ('fries',     'fat'):      19,
    ('fries',     'sodium'):   270,
    ('macaroni',  'calories'): 320,
    ('macaroni',  'protein'):  12,
    ('macaroni',  'fat'):      10,
    ('macaroni',  'sodium'):   930,
    ('pizza',     'calories'): 320,
    ('pizza',     'protein'):  15,
    ('pizza',     'fat'):      12,
    ('pizza',     'sodium'):   820,
    ('salad',     'calories'): 320,
    ('salad',     'protein'):  31,
    ('salad',     'fat'):      12,
    ('salad',     'sodium'):   1230,
    ('milk',      'calories'): 100,
    ('milk',      'protein'):  8,
    ('milk',      'fat'):      2.5,
    ('milk',      'sodium'):   125,
    ('ice cream', 'calories'): 330,
    ('ice cream', 'protein'):  8,
    ('ice cream', 'fat'):      10,
    ('ice cream', 'sodium'):   180}

求达到足够营养花费的代价最小。

# STEP: 创建模型
m = gp.Model("diet")

# STEP: 购买多少
buy = m.addVars(foods, name="buy")
# buy = {}
# for f in foods:
#   buy[f] = m.addVar(name=f)

# STEP: 设置目标函数，下标相同相乘可用prod函数
m.setObjective(buy.prod(cost), GRB.MINIMIZE)
# m.setObjective(sum(buy[f]*cost[f] for f in foods), GRB.MINIMIZE)

# STEP: 添加约束
m.addConstrs((gp.quicksum(nutritionValues[f, c] * buy[f] for f in foods)
             == [minNutrition[c], maxNutrition[c]]
             for c in categories), "_")
# for c in categories:
#  m.addRange(sum(nutritionValues[f, c] * buy[f] for f in foods),
#             minNutrition[c], maxNutrition[c], c

最后创建打印函数，并执行：

def printSolution():
    if m.status == GRB.OPTIMAL:
        print('\nCost: %g' % m.ObjVal)
        print('\nBuy:')
        for f in foods:
            if buy[f].x > 0.0001:
                print('%s %g' % (f, buy[f].x))
    else:
        print('No solution')


# Solve
m.optimize()
printSolution()

print('\nAdding constraint: at most 6 servings of dairy')
m.addConstr(buy.sum(['milk', 'ice cream']) <= 6, "limit_dairy")

# Solve
m.optimize()
printSolution()